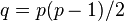نظریه گراف شاخهای از ریاضیات است که دربارهٔ گرافها بحث میکند. این مبحث در واقع شاخهای از توپولوژی است که با جبر و نظریه ماتریسها پیوند مستحکم و تنگاتنگی دارد. نظریهٔ گراف برخلاف شاخههای دیگر ریاضیات نقطهٔ آغاز مشخصی دارد و آن انتشار مقالهای از لئونارد اویلر، ریاضیدان سوئیسی، برای حل مسئله پلهای کونیگسبرگ در سال ۱۷۳۶ است.
پیشرفتهای اخیر در ریاضیات، به ویژه در کاربردهای آن موجب گسترش چشمگیر نظریهٔ گراف شده است.
به گونهای که هماکنون نظریهٔ گراف ابزار بسیار مناسبی برای تحقیق در زمینههای گوناگون مانند نظریه کدگذاری، تحقیق در عملیات، آمار، شبکههای الکتریکی، علوم رایانه، شیمی،زیستشناسی، علوم اجتماعی و سایر زمینهها گردیده است.
تاریخچه ی نظریه گراف:
برخلاف شاخههای دیگر ریاضیات، سیر نظریهٔ گراف آغاز معینی در زمان و مکان دارد و آن مسئلهٔ هفت پل کونیگسبرگ است که در سال ۱۷۳۶ توسط لئونارد اویلر حل شد. در سال ۱۷۵۲ قضیهٔ اویلر برای گرافهای مسطح ارائه میشود. اما پس از آن به مدت تقریباً یک قرن فعالیت اندکی در این زمینه صورت گرفت.
در سال ۱۸۴۷، گوستاو کیرشهف نوع خاصی از گرافها به نام درخت را مورد بررسی قرار داد. کیرشهف این مفهوم را هنگام تعمیم قوانین اهم برای جریان الکتریکی در کاربردهایی که حاوی شبکههای الکتریکی بودند بهکار گرفت. ده سال بعد، آرتور کیلی همین نوع گراف را برای شمارش ایزومرهای متمایز هیدروکربنهای اشباع شدهٔ CnH۲n+۲  بهکار برد.
بهکار برد.
در همین دوران شاهد حضور دو ایدهٔ مهم دیگر در صحنه هستیم. ایدهٔ اول حدس چهار رنگ بود که نخستین بار توسط فرانسیس گوثری در حدود سال ۱۸۵۰ مورد تحقیق قرار گرفت. این مسئله سرانجام در سال ۱۹۷۶، توسط کنث ایپل و ولفگانگ هیکن و با استفاده از یک تحلیل رایانهای پیچیده حل شد.
ایدهٔ مهم دوم، دور همیلتونی بود. این دور به افتخار سر ویلیام روآن همیلتون نامگذاری شده است. او این ایده را در سال ۱۸۵۹ برای حل معمای جالبی حاوی یالهای یک دوازده وجهی منتظم بهکار گرفت. یافتن جوابی برای این معما چندان دشوار نیست ، ولی ریاضیدانان هنوز در پی یافتن شرایطی لازم و کافی هستند که گرافهای بیسوی حاوی مسیر یا دورهای همیلتونی را مشخص کنند.
پس از این کارها تا بعد از سال ۱۹۲۰ فعالیت اندکی در این زمینه صورت گرفت. مسئلهٔ مشخص کردن گرافهای مسطح را کازیمیر کوراتوفسکی، ریاضیدان لهستانی، در سال ۱۹۳۰ حل کرد. نخستین کتاب دربارهٔ نظریهٔ گراف در سال ۱۹۳۶ منتشر شد. این کتاب را ریاضیدان مجار، دنش کونیگ، که خود محقق برجستهای در این زمینه بود، نوشت. از آن پس فعالیتهای بسیاری در این زمینه صورت گرفته و رایانه نیز در چهار دههٔ اخیر به یاری این فعالیتها آمده است.
تعریف:
یک گراف از مجموعهای غیر خالی از اشیاء به نام رأس تشکیل شده، که آن را با  نشان میدهیم، و مجموعهای شامل یالها، که رأسها را به هم وصل میکنند و با
نشان میدهیم، و مجموعهای شامل یالها، که رأسها را به هم وصل میکنند و با  نمایش میدهیم. یک چنین گرافی را با
نمایش میدهیم. یک چنین گرافی را با  نشان میدهیم. اگر یال
نشان میدهیم. اگر یال  دو رأس
دو رأس 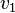 و
و 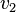 را به هم وصل کند مینویسیم
را به هم وصل کند مینویسیم  .[۳]
.[۳]
اندازه گراف:
اندازه گراف تعداد یالهای یک گراف است و به صورت  بیان میشود.
بیان میشود.
درجه راسها:
در نظریه گرافها، درجه یک راس به تعداد یالهای متصل به آن راس گفته میشود. به عبارت دیگر، درجه یک راس تعداد همسایگی (مجاورت)های مستقیم یک راس را بیان میکند. از آنجا که هر یال در گراف دو راس را به هم وصل میکند، مجموع درجه راسهای یک گراف با دو برابر تعداد یالهای ان گراف برابر است.
انواع گراف:
گراف همبند گرافی است که بین همه ی راسهای آن مسیری وجود داشته باشد.
گراف کامل:

در نظریه گراف، یک گراف کامل، گرافیاست که بین هر دو راس آن دقیقاً یک یال وجود داشته باشد. یک گراف کامل از مرتبه n، دارای n راس و 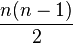 یال است که آن را با
یال است که آن را با 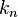 نشان میدهند. یک گراف کامل یک گراف منتظم از درجه n-۱ است.
نشان میدهند. یک گراف کامل یک گراف منتظم از درجه n-۱ است.
گرافهای کاملی که p≥3 قطعاً همیلتونی هستند.
گرافهای کاملی که p≥3 و p فرد باشد ( p=2k+1) اویلری هستند، چون درجه ی هر راس زوج است.
گراف پترسن:
گراف پترسن گرافی با ۱۰ راس و ۳- منتظم است که به صورت زیر رسم میگردد:
گراف دو بخشی:
مفهوم شهودی:

فرض کنید در یک شرکت صنعتی تعدادی شغل بدون متصدی میباشند و تعدادی متقاضی برای این مشاغل اعلام آمادگی نمودهاند. حال این سوال مطرح میشود که آیا میتوان به هر متقاضی شغلی متناسب او اختصاص داد؟ برای حل چنین مسئلهای که به مسئلهٔ تخصیص موسوم است، با استفاده از گراف میتوان وضعیتهای خاص را پیاده سازی نمود. بدین ترتیب که گروهی که متقاضی مشاغل هستند در مجموعهای به نام X و مجموعه مشاغل بدون متصدی را در مجموعهای به نام Y قرار میدهیم. گراف رسم شده چنین است که به بعضی از اعضای مجموعه X یک یا چند عضو از مجموعه Y توسط یالها وصل مینماید. به عبارت دیگر گراف بوجود امده دارای یالهای xy است که هر متقاضی x را از مجموعه X به شغلهای مناسب y از مجموعه Y متصل مینماید. به عبارت دقیقتر هیچ دو راس متعلق به مجموعه X (متفاضیان) یا هیچ دو راس متعلق به مجموعه Y (مشاغل) توسط هیچ یالی به هم متصل نمیباشند. چنین گرافی را گراف دوبخشی یا دوپارچه میگویند.
تعریف گراف دوبخشی:
گراف دوبخشی گرافی است که بتوان مجموعه رئوس آن را به دو مجموعه X و Y چنان افراز نمود که هر یال آن دارای یک انتها در X و یک انتها در Y باشد، به گونهای که هیچ دوراسی در X یا در Y با هم مجاور نباشند. چنین افرازی را دوبخشی کردن گراف مینامند.
- یادآوری: منظور از افراز یک مجموعه چون A به چند مجموعه، تقسیم مجموعه A به چند مجموعه ناتهی دیگر است که باهم اشتراکی نداشته باشند و اجتماع همه آنها برابر مجموعه A باشد. و در اینجا اگر V به عنوان مجموعه رئوس باشد افراز V به دو مجموعه X و Y (ناتهی) به این صورت است که: X
 Y = V و X
Y = V و X Y =
Y = 
- مثال
به عنوان مثال گراف زیر یک گراف دو بخشی است:
گراف ساده:
گراف ساده: هر گراف G زوج مرتبی مانند (V,E) است که در آن V مجموعهای متناهی و ناتهی است و E زیرمجموعهای از تمام زیرمجموعههای دو عضوی V میباشد. اعضای V را رأسهای G و اعضای E را یالهای G مینامیم. به بیان ساده تر بین دو رأس یک گراف ساده حداکثر یک یال وجود دارد و هیچ طوقهای (یعنی یالی که رأس را به خودش وصل میکند) نیز وجود نداشته باشد.[۴]
گراف همیلتونی:
گراف ساده ی G از مرتبه V هرگاه دوری به طول V در آن یافت شود.
گراف چرخ:
هر گراف G که دارای n راس باشد کهn≥۴ و یکی از رئوس از درجهٔ n-۱ و بقیه از درجهٔ سه باشند، را یک گراف چرخ مینامیم- مانند مثالهای زیر:
گراف چرخn راسی را با nW نمایش میدهیم.
گراف چندگانه:
گراف چندگانه: هرگاه بین دو رأس متمایز از یک گراف بیش از یک یال وجود داشته باشد، آن را یک گراف چند گانه میگوییم.
گراف مکعبی:
یک گراف «k مکعب» (k-Cube) گرافی است که رئوس آنk تایی از «صفر» و «یک» هستند که دو رأس آن به یکدیگر متصل هستند اگر و فقط اگر دو رأسشان دقیقاً در یک مؤلفه با یکدیگر تفاوت داشته باشند. بهعبارت دیگر اگر kعددی طبیعی باشد منظور از «kمکعب» گرافی است که رأسهای آن همهٔ دنبالههای رقمی از «صفر» و «یک» هستند و دو رأس در این گراف مجاور بوده هرگاه دنبالههای متناظرشان دقیقاً در یک مؤلفه اختلاف داشته باشند (شکل ۱).
میتوان نشان داد که یک گراف «k مکعب» (k-Cube) دارای ویژگیهایی نظیر ذیل است:
- تعداد رؤوس =۲k
- تعداد یالها=k*۲(k-۱)
- گرافی «دوبخشی» (Bipartite) است.
گراف جهت دار:
گراف جهت دار: هر گراف G زوج مرتبی مانند (V,E) است که در آن V مجموعهای متناهی و ناتهی است و E زیرمجموعهای از مجموعهٔ تمام زوج مرتبهای متشکل از اعضای V است.
گراف جهتدارو کاربردهای آن:
گراف جهت دارو کاربردهای آنگراف جهت دار D، یک سه تایی مرتب(O(D) و A(D) و (V(D)است که تشکیل شده از یک مجموعه ناتهی V(D) از راسها ویک مجموعه (D) A مجزای از V(D)از کمانها و یک تابع وقوع O(D)که به هر کمان D یک زوج مرتب از راسهای D- که الزاماً متمایز نیستند- را نسبت میدهد. اگر a یک کمان وu,v دو راس باشند به طوری که(u,v) =(a)O (D)، آنگاه میگوئیم که u,a را به v وصل کرده است؛ u، دم v,a سرa نامیده میشود.
گراف مسطح:
گراف مسطح: گراف مسطح گرافی است که میتوان آن را در یک صفحه محاط کرد به گونهای که یالهایش یکدیگر را تنها در راسها قطع کنند. به این گراف هامنی نیز گفته میشود.
در بین گرافهای کامل فقط گرافهایی با تعداد راس مساوی یا کمتر از 5 (p≤5) را، میتوان به صورت مسطح رسم کرد.
گراف وزن دار:
گراف وزن دار: در یک گراف وزن دار، به هر یال یک وزن (عدد) نسبت داده میشود. معمولاً اعداد حقیقی به عنوان وزن یالها استفاده میشوند. اما بسیاری از الگوریتمهای پر کاربرد فقط برای گرافهایی که دارای وزن صحیح یا مثبت هستند طراحی شدهاند.
خصوصیات گرافهای خاص:
- اگر درجهٔ همهٔ راسها در گراف ساده با هم برابر و برابر بزرگترین درجهٔ ممکن (یعنی p-۱) باشد، گراف مورد نظر منتظم کامل است. در این گونه گرافها، رابطهٔ میان رأسها و یالها چنین است:
- که در آن
 تعداد راسها، و
تعداد راسها، و  تعداد یالها است.
تعداد یالها است.
- اگر گراف همبند باشد (یعنی از هر نقطه بتوان به یک نقطه دلخواه دیگر رسید) ولی دور نداشته باشد (یعنی هیچ نقطهای از دوراه به نقطهٔ بعدی نرسد) میگویند گراف درختی است. در اینگونه گرافها فرمول زیر صدق میکند (شرط لازم):
- که در آن
 تعداد رأسها، و
تعداد رأسها، و  تعداد یالها است.[۵]
تعداد یالها است.[۵]
- گراف اویلری و همیلتونی:گاهی اوقات ما میخواهیم در یک گراف حرکت کنیم. به اینصورت که از راسی به راسی دیگر برویم. در اینصورت ممکن است برای ما مهم باشد که از روی یال یا راس تکراری حرکت نکنیم(مشابه مسالهٔ فروشندهٔ دوره گرد). این مساله در صرفه جویی زمان و هزینه هم مهم است.(یعنی مبحث بهینه سازی). دراینجا دو موضوع گرافهای اویلری(دور زدن در گراف بدون یال تکراری)و همیلتونی(دور زدن بدون راس تکراری) مطرح میشود. براحتی میتوان بررسی کرد که راسهای گراف اویلری باید درجهٔ زوج داشته باشند. اما اینکه شرایط کامل لازم و کافی برای همیلتونی بودن یک گراف چیست هنوز حل نشده ماندهاست.
کاربردها:
از گرافها برای حل مسایل زیادی در ریاضیات و علوم کامپیوتر استفاده میشود. ساختارهای زیادی را میتوان به کمک گرافها به نمایش در آورد. برای مثال برای نمایش چگونگی رابطه وب سایتها به یکدیگر میتوان از گراف جهت دار استفاده کرد. به این صورت که هر وب سایت را به یک راس در گراف تبدیل میکنیم و در صورتیکه در این وب سایت لینکی به وب سایت دیگری بود، یک یال جهت دار از این راس به راسی که وب سایت دیگر را نمایش میدهد وصل میکنیم.
از گرافها همچنین در شبکهها، طراحی مدارهای الکتریکی، اصلاح هندسی خیابانها برای حل مشکل ترافیک، و.... استفاده میشود. مهمترین کاربرد گراف مدلسازی پدیدههای گوناگون و بررسی بر روی آنهاست. با گراف میتوان به راحتی یک نقشه بسیار بزرگ یا شبکهای عظیم را در درون یک ماتریس به نام ماتریس وقوع گراف ذخیره کرد و یا الگوریتمهای مناسب مانند الگوریتم دایسترا یا الگوریتم کروسکال و... را بر روی آن اعمال نمود. در این جا به بررسی گرافهایی میپردازد که میتوان آنها را به نحوی روی صفحه کشید که یالها جز در محل راسها یکدیگر را قطع نکنند. این نوع گراف در ساخت جادهها و حل مساله کلاسیک و قدیمی سه خانه و سه چاه آب به کار میرود.
کاربرد گراف بازهها از گرافها برای حل مسایل زیادی در ریاضیات و علوم کامپیوتر استفاده میشود. ساختارهای زیادی را میتوان به کمک گرافها به نمایش در آورد.
درخت و ماتریس درخت در رشتههای مختلفی مانند شیمی مهندسی برق و علم محاسبه کاربرد دارد. کیرشهف در سال ۱۸۴۷ میلادی هنگام حل دستگاههای معادلات خطی مربوط به شبکههای الکتریکی درختها را کشف و نظریه درختها را بارور کرد. کیلی در سال ۱۸۵۷ میلادی درختها را در ارتباط با شمارش ایزومرهای مختلف هیدروکربنها کشف کرد وقتی مثلا میگوییم در ایزومر مختلف c4h۱۰ وجود دارد منظورمان این است که دو درخت متفاوت با ۱۴ راس وجود دارند که درجه ۴ راس از این ۱۴ راس جهار و درجه هر یک از ۱۰ راس باقیمانده یک است. اگر هزینه کشیدن مثلا راه آهن بین هر دو شهر ازp شهر مفروض مشخص باشد ارزانترین شبکهای که این p شهر را به هم وصل میکند با مفهوم یک درخت از مرتبه p ارتباط نزدیک دارد. به جای مساله مربوط به راه آهن میتوان وضعیت مربوط به شبکههای برق رسانی و لوله کشی نفت و لوکشی گاز و ایجاد کانالهای آبرسانی را در نظر گرفت. برای تعیین یک شبکه با نازلترین هزینه از قاعدهای به نام الگوریتم صرفه جویی استفاده میشود که کاربردهای فراوان دارد. از گرافها میتوان به عنوان کدهای کمکی نام برد که به DVB Playerها در بالا بردن قابلیتهای آنها کمک میکنند. گرافها دارایی مزایای مختلفی هستند که شفاف تر کردن و واضحتر کردن تصویر و کاهش مصرف CPU به عنوان یکی از اصلیترین مزایای آنها بشمار میرود.
تعریف گراف:
تعریف دقیقتر گراف به این صورت است، که گراف مجموعهای از رأسها است، که توسط خانوادهای از زوجهای مرتب که همان یالها هستند به هم مربوط (وصل) شدهاند.
یالها بر دو نوع ساده و جهت دار هستند، که هر کدام در جای خود کاربردهای بسیاری دارد. مثلاً اگر صرفاً اتصال دو نقطه -مانند اتصال تهران و زنجان با کمک آزادراه- مد نظر شما باشد، کافیست آن دو شهر را با دو نقطه نمایش داده، و اتوبان مزبور را با یالی ساده نمایش دهید. اما اگر بین دو شهر جادهای یکطرفه وجود داشته باشد آنگاه لازمست تا شما با قرار دادن یالی جهت دار مسیر حرکت را در آن جاده مشخص کنید. همچنین برای اینکه فاصله بین دو شهر را در گراف نشان دهید، میتوانید از گراف وزن دار استفاده کنید و مسافت بین شهرها را با یک عدد بر روی هر یال نشان دهید.
آغاز نظریهٔ گراف به سدهٔ هجدهم بر میگردد. اولر ریاضیدان بزرگ مفهوم گراف را برای حل مسئله پلهای کونیگسبرگ ابداع کرد اما رشد و پویایی این نظریه عمدتاً مربوط به نیم سدهٔ اخیر و با رشد علم انفورماتیک بودهاست.
مهمترین کاربرد گراف مدلسازی پدیدههای گوناگون و بررسی بر روی آنهاست. با گراف میتوان به راحتی یک نقشه بسیار بزرگ یا شبکهای عظیم را در درون یک ماتریس به نام ماتریس وقوع گراف ذخیره کرد و یا الگوریتمهای مناسب مانند الگوریتم دایجسترا یا الگوریتم کروسکال و... را بر روی آن اعمال نمود.
یکی از قسمتهای پرکاربرد نظریهٔ گراف، گراف مسطح است که به بررسی گرافهایی میپردازد که میتوان آنها را به نحوی روی صفحه کشید که یالها جز در محل راسها یکدیگر را قطع نکنند. این نوع گراف در ساخت جادهها و حل مساله کلاسیک و قدیمی سه خانه و سه چاه آب به کار میرود.
نظریه گراف یکی از پرکاربردترین نظریهها در شاخههای مختلف علوم مهندسی (مانند عمران)، باستانشناسی (کشف محدوده یک تمدن) و... است.
روابط میان راسهای یک گراف را میتوان با کمک ماتریس بیان کرد.
برای نمایش تصویری گرافها معمولاً از نقطه یا دایره برای کشیدن راسها و از کمان یا خط راست برای کشیدن یال بین راسها استفاده میشود.
منبع: دانشنامه آزاد ویکی پدیا [فارسی]