اندازه در ریاضیات، به تابعی گفته می‌شود، که یک عدد یا مقدار را (به عنوان مثال اندازه، حجم یا احتمال) به هر زیرمجموعه از یک مجموعه خاص، نسبت می‌دهد. این نظریه به منظور، محاسبه انتگرالها بر روی مجموعه‌ها به جای برروی فاصله‌ها (یا همان بازه‌ها) که در معمول انجام می‌پذیرد، گسترش پیدا کرد و از این رو در آنالیز ریاضی و در نظریه احتمالات، بسیار دارای اهمیت می‌باشد.

نظریه اندازه، قسمت مهمی از آنالیز حقیقی است، به طوری که جبرهای سیگما، قیاس‌ها توابع قیاس‌پذیر و انتگرالها را مورد تحقیق، قرار می‌دهد و در نظریه احتمالات و آمار از اهمیت زیادی برخوردار است.

تعریف:

برطبق تعریف، اندازه u تابعی است (یا به عبارتی نگاشتی است)، که برروی سیگما جبر بر مجموعه X، تعریف می‌شود و مقادیر بین ، می‌پذیرد و دارای خصوصیت‌های زیر است:

در اینجا مجموعه تهی و تعداد شمارایی از مجموعه‌هایی در هستند، که اشتراک هرکدام از آنها با دیگری تهی است (مجموعه‌ها مجزا هستند). در این حالت به 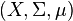فضای اندازه‌ای و به اعضای ، مجموعه‌های اندازه‌پذیر گفته می‌شود.