آخرین قضیه فرما، قضیه اولین بار توسط فرما در فرم توجه داشته باشید نوشته شده در حاشیه از کپی خود از یونان باستان متن Arithmetica توسط دیوفانت پیشنهاد شده است. توجه داشته باشید نوشته شده پس از مرگ نویسنده کشف شد و در حال حاضر از دست داده است. با این حال، یک کپی در یک کتاب منتشر شده توسط پسر فرما حفظ شد. توجه داشته باشید، فرما ادعا به اثبات را کشف کرده اند که معادله سیاله هیچ عدد صحیح راه حل برای و است.

متن کامل بیانیه فرما، در زبان لاتین نوشته شده است، می خواند "autem Cubum در، duos cubos، دانشگاه صنعتی امیرکبیر quadrato quadratum در quadrato-quadratos، نشان generaliter nullam در بی نهایت فوق العاده quadratum potestatem در duos eiusdem nominis FAS EST dividere cuius ترویج demonstrationem mirabilem عاقل detexi duos Hanc marginis exiguitas غیر caperet "(Nagell 1951، ص 252). در ترجمه، "این غیر ممکن است برای یک مکعب به عنوان مجموع دو مکعب، یک قدرت چهارم به عنوان مجموع دو قدرت چهارم، و یا به طور کلی برای هر عدد است که یک قدرت بزرگتر از دومی به عنوان مجموع دو مانند قدرت من را کشف کرده اند یک تظاهرات واقعا شگفت انگیز و جادویی این گزاره که این حاشیه خیلی تنگ شده داشته باشد. "

به عنوان یک نتیجه از حاشیه توجه داشته باشید فرما، قضیه که معادله سیاله

(1)

جایی که ، ، و اعداد صحیح است، هیچ راه حل برای غیر صفر آمده است به عنوان تاریخ و زمان آخرین قضیه فرما شناخته می شوند. آن را "نامیده می شد قضیه "قدرت بیانیه فرما است، با وجود این واقعیت است که هیچ ریاضیدان دیگری قادر به آن را اثبات کند برای صدها سال بود.

توجه داشته باشید که محدودیت واضح است که لازم است از آنجا که تعدادی از فرمول ابتدایی وجود دارد برای تولید تعداد نامحدود از سه فیثاغورس رضایت بخش معادله برای ،

(2)

اولین تلاش برای حل معادله می تواند با تلاش با فاکتور معادله ساخته شده، به

(3)

از آنجا که محصول دقیق قدرت ،

(4)

حل و می دهد

(5)

که به

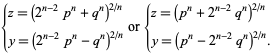(6)

با این حال، از آنجا که راه حل هایی برای این معادلات در اعداد گویا هستند آسان تر برای پیدا کردن از راه حل های معادله اصلی، این رویکرد متاسفانه هیچ بینش اضافی فراهم نمی کند.

اگر یک فرد نخست تقسیم ، و سپس کاهش

(7)

را می توان ساخته شده است، بنابراین تعریف جدیدی استدلال می دهد

(8)

اگر هیچ فرد نخست تقسیم ، و سپس توانی از 2 است، بنابراین و در این مورد، معادلات ( 7 ) و ( 8 ) کار با 4 در محل است. از آنجا که مورد توسط فرما ثابت شد به هیچ راه حل، آن را به اثبات آخرین قضیه فرما با توجه به عجیب و غریب کافی است فقط قدرت نخست .

به طور مشابه، با در نظر گرفتن فقط کافی برای اثبات آخرین قضیه فرما است نسبتا نخست ، و از آنجا که هر واژه در معادله (1) پس از آن می توانید با تقسیم شود که در آن بزرگترین مقسوم علیه مشترک است .

به اصطلاح "مورد اول" از قضیه برای شارحان هستند که نسبتا نخست ، و ( ) و توسط Wieferich در نظر گرفته شد. سوفی ژرمن ثابت اولین مورد از آخرین قضیه فرما برای هر فرد نخست وقتی که همچنین نخست . لژاندر پس از آن ثابت کرد که اگر نخست به طوری که ، ، ، ، یا نخست ، پس از آن اولین مورد از آخرین قضیه فرما نگه می دارد است. این فرما تاسیس شده و زمان آخرین قضیه است. در سال 1849، ادوارد کومر آن را برای همه ثابت به طور منظم اعداد اول و اعداد مرکب که آنها عوامل (Vandiver سال 1929، توپ و Coxeter 1987).

"حالت دوم" قضیه آخر فرما " تقسیم دقیقا یکی از ، ، است. توجه داشته باشید که است که توسط حکومت ، ، نسبتا نخست، و اگر دو تا از تقسیم ، ، ، سپس آن را نیز تقسیم سوم، معادله ( 8 ).

حمله از ادوارد کومر منجر به نظریه ایده آل ، و Vandiver به توسعه معیارهای Vandiver برای تصمیم گیری اگر با توجه به نامنظم نخست ارضا قضیه. در سال 1852، Genocchi ثابت کرد که مورد اول درست است اگر یک جفت نامنظم . در سال 1858، ادوارد کومر نشان داد که در مورد اول درست است، اگر هر یا جفت نامنظم ، که پس از آن که شامل تمدید شد و توسط Mirimanoff (1909). Vandiver (1920ab) اشاره کرد از شکاف ها و اشتباهات در خاطرات ادوارد کومر که در نظر او، از درجه اعتبار ساقط اثبات قضیه آخرین فرما برای با اعداد اول نامنظم 37، 59، و 67 ادوارد کومر، اگر چه او ادعا اثبات FLT Mirimanoff توان 37 هنوز هم معتبر است.

Wieferich (1909) ثابت کرد که اگر معادله در اعداد صحیح حل نسبتا نخست نخست عجیب و غریب ، و سپس

(9)

(توپ و Coxeter 1987). این اعداد به نام اعداد اول Wieferich . Mirimanoff (1909) پس از آن نشان داد که

(10)

همچنین باید برای راه حل های برگزاری نسبتا نخست نخست عجیب و غریب ، که مانع از دو مورد اول اعداد اول Wieferich 1093 و 3511. در سال 1914، Vandiver نشان داد

(11)

و Frobenius از این تمدید به

(12)

آن را نیز نشان داده شده است که اگر نخست از فرم ، و سپس

(13)

که کوچکترین ممکن مطرح در "مورد اول" را به توسط 1941 (Rosser 1941). گرانویل و Monagan (1988) نشان داد که اگر وجود داشته باشد وجود دارد نخست رضایت آخرین قضیه فرما، و سپس

(14)

برای ، 7، 11، ...، 71. این ثابت می کند که مورد اول برای همه درست است نخست شارحان تا (وردی، 1991).

"حالت دوم" تاریخ و زمان آخرین قضیه فرما (برای ) ثابت سخت تر از مورد اول است.

اویلر ثابت حالت کلی از قضیه برای ، فرما ، دیریکله و لاگرانژ است. در سال 1832 دیریکله تاسیس مورد است. مورد توسط لنگ (1839. ولز، سال 1986، ص 70) ثابت شد، با استفاده از هویت

(15)

اگرچه برخی از اشتباهات در این اثبات حضور داشتند، این پس از آن توسط Lebesgue در سال 1840 ثابت شد. پیشرفت های اضافی بسیار بیش از 150 سال آینده ساخته شده بود، اما هیچ نتیجه ای کاملا به طور کلی به دست آمده است. تقویت اعتماد به نفس کاذب پس از اثبات خود را که پی متعالی ، ریاضیدان Lindemann اقدام به انتشار چند اثبات آخرین قضیه فرما، همه آنها را نامعتبر است (بل 1937، ص 464-465). جایزه مارک های آلمانی، شناخته شده به عنوان جایزه Wolfskehl ، نیز برای اولین مدرک معتبر (. Barner 1997؛ هافمن 1998، صص 193-194 و 199 توپ و Coxeter سال 1987، ص 72) ارائه شده است.

یک هشدار اشتباه اخیر برای یک اثبات کلی ارائه توسط Y. Miyaoka (Cipra 1988) که اثبات، با این حال، معلوم شد که ناقص مطرح شد. سایر اثبات تلاش در میان ریاضیدانان هر دو حرفه ای و آماتور VOS SAVANT (1993) مورد بحث، اگر چه VOS SAVANT به اشتباه ادعا می کند که کار بر روی این مشکل توسط نیرنگ (بحث شده در زیر) نامعتبر است. با زمان 1993 در اطراف نورد، حالت کلی از تاریخ و زمان آخرین قضیه فرما نشان داده شده بود که برای همه شارحان واقعی تا (Cipra 1993). به هر حال، با توجه به که نیاز به اثبات آخرین قضیه فرما برای همه شارحان حقیقت، اثبات برای هر تعداد از شارحان محدود می کند به سمت اثبات قضیه به طور کلی هر گونه پیشرفت قابل توجهی را تشکیل می دهند نه (هر چند واقعیت که هیچ نقضی برای این بسیاری از موارد یافت شد بسیار مطرح).

در سال 1993، بمب کاهش یافته بود. در آن سال، قضیه به طور کلی تا حدی به توسط اندرو نیرنگ (Cipra سال 1993، استوارت 1993) با اثبات ثابت شد semistable مورد از حدس Taniyama Shimura . متاسفانه، چند سوراخ در اثبات کشف شد و مدت کوتاهی پس از آن زمانی که رویکرد نیرنگ طریق حدس Taniyama Shimura بر خواص آویزان شد گروه Selmer با استفاده از یک ابزار به نام سیستم اویلر است . با این حال، مشکل با نیرنگ و R. تیلور در اواخر سال 1994 دور شد (سال 1994، Cipra 1995) و در تیلور و نیرنگ (1995) و نیرنگ (1995) منتشر شده است. اثبات نیرنگ موفق (1) جایگزین کردن منحنی های بیضوی با نمایندگی گالوا، (2) کاهش مشکل به شماره فرمول کلاس ، (3) اثبات می کند که فرمول ، و (4) مقید کردن شل به پایان می رسد که بوجود می آیند زیرا شکل های در شکست ساده ترین موارد (Cipra 1995) انحطاط.

اثبات آخرین قضیه فرما نشانه پایان یک دوره ریاضی. از آنجا که تقریبا تمام ابزار که در نهایت آورده بودند به تحمل مشکل تا به حال هنوز به در زمان فرما اختراع جالب برای حدس و گمان در مورد اینکه آیا او در واقع در اختیار داشتن یک اثبات قضیه از ابتدایی بود. قضاوت توسط سرسختی است که با مشکل حمله برای مدت طولانی در برابر، اثبات ادعا فرما به نظر می رسد به احتمال زیاد به وهم بوده است. این نتیجه گیری است که بیشتر توسط این واقعیت است که فرما برای اثبات موارد جستجو و ، که می شده اند اضافی بود که او در واقع در اختیار داشتن یک اثبات کلی ارائه شده است.

در قسمت از برنامه تلویزیونی سیمپسونها، معادله به نظر می رسد در یک نقطه در پس زمینه. توسعه نشان می دهد که تنها 9 رقم اعشار اولین مسابقه (راجرز 2005). قسمت جادوگر تراس همیشه سبز اشاره که منطبق نه تنها در 10 رقم اعشار برای اولین بار، بلکه آسان به چک کردن آخرین جایی (Greenwald). در آغاز از پیشتازان فضا: زمان ایجاد قسمت بعدی "رویال" کاپیتان پیکارد، اشاره می کند که مطالعه تاریخ و زمان آخرین قضیه فرما یک فرایند آرامش بخش است.