قوانین حساب های مجتمع

- هر عدد مختلط `` فرم استاندارد''

برای برخی از واقعی و ب.
- برای واقعی و b،



تقسیم
توجه داشته باشید که در قوانین 4 و 5 دولت که ما نمی توانیم از اعداد مختلط با اضافه کردن یا تفریق یا ضرب دو عدد مختلط با یکدیگر. در مورد تقسیم یک عدد مختلط دیگر چه؟ آیا نتیجه دیگری عدد مختلط است؟ اجازه دهید این سوال را در راه دیگری بپرسید. اگر چهار عدد واقعی شما داده می شود A، B، C و D، می تواند به شما پیدا کردن دو نفر دیگر اعداد حقیقی x و y به طوری که
![]()
به عنوان یک ورزش با استفاده از قوانین 1 تا 5، ضرب هر دو طرف معادله فوق توسط c + DI و سپس حل برای x و y ثابت کند که پاسخ به پرسش ما این است: بله (با کلیک بر روی کمک برای راه حل.)
خوب، پس ما می توانیم توسط c + دی تقسیم اگر c و d هر دو صفر نیست. اما یک راه بسیار ساده تر به انجام تقسیم بندی وجود دارد.
توجه داشته باشید که
![]()
ما می گوییم که C + DI و c - دی ترکیبات پیچیده هستند. برای ساده کردن یک کسر پیچیده، ضرب صورت کسر و مخرج مزدوج مختلط مخرج.
نمونه هایی از تقسیم
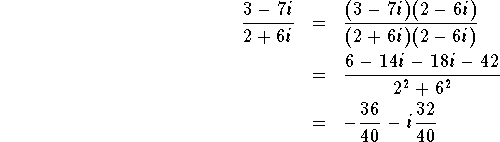


قسمت حقیقی و موهومی
اگر z = + دو عدد مختلط است و a و b واقعی هستند، به ما می گویند که بخشی واقعی از z است و آن ب بخش موهومی Z است و ما می نویسیم
![]()
ورزش:
پیدا کردن ![]() و
و ![]() (راه حل)
(راه حل)
Conjugates می مجتمع
اگر z = + دو عدد مختلط با بخش واقعی و بخش موهومی ب، پس از آن ما مزدوج مختلط Z معنی شده توسط ![]() است.
است.
ورزش:
نوشتن ![]() در فرم استاندارد.
در فرم استاندارد.
(راه حل)
ورزش:
ثابت کنیم که ![]() برای هر جفت از اعداد مختلط است و به همین ترتیب
برای هر جفت از اعداد مختلط است و به همین ترتیب ![]() است.
است.
(Proof.)
ورزش:
ثابت کنیم که ![]() برای هر عدد صحیح N.
برای هر عدد صحیح N.
(Proof.)
مدول عدد مختلط
قدر یا مدول عدد مختلط z مشخص | Z | و تعریف شده به عنوان
![]()
توجه داشته باشید که ![]() (proof.).
(proof.).
ورزش:
ثابت کنیم که ![]() (راه حل)
(راه حل)


