در ریاضیات قضیه خوش‌ترتیبی، قضیه‌ای است که می‌گوید هر مجموعه می‌تواند خوش‌ترتیب باشد. با اصل خوش‌ترتیبی فرق دارد ولی گاهی از آن به عنوان اصل خوش‌ترتیبی یاد شده است.

ارنست زرملو از اصل انتخاب استفاده کرد تا این قضیه را به عنوان یک اصل منطقی غیر قابل رد معرفی کرد که منجر به اثبات هم ارزی اصل انتخاب و قضیه خوش‌ترتیبی شد.

اثبات این قضیه یک رابطه خوش‌ترتیب و چگونگی آن را معرفی نمی‌کند تنها اثبات می‌کند که برای هر مجموعه، رابطه‌ای خوش ترتیب وجود دارد. در حالی که بسیاری از ریاضی‌دانان برای مجموعه‌ای چون اعداد حقیقی یک رابطه خوش‌ترتیب را غیر قابل تصور می‌دانند.

اصل خوش ترتیبی:

 اصل خوشترتیبی بیان می کند هر زیر مجموعه ناتهی از مجموعه اعداد طبیعی دارای عضو ابتدا یا کوچکترین عضو است. 
به عبارت دیگر: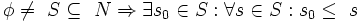 
 
یا به عبارت دیگر وجود دارد 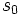 به گونه ای که: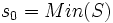  

با استفاده از اصل خوشترتیبی نتایج زیر حاصل می شود که می توان آنها را تعمیمی بر این اصل دانست: 

1- هر زیر مجموعه ناتهی و از پایین کراندار از مجموعه اعداد صحیح دارای عضو مینیمم(کوچکترین عضو یا عضو ابتدا) 
است. 

برهان: 

فرض می کنیم مجموعه S زیر مجموعه ای ناتهی از مجموعه اعداد صحیح و از پایین کراندار باشد و 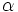 یک کران پایین آن باشد یعنی: 
مجموعه T را به این صورت تعریف می کنیم: 
 
چون S ناتهی است پس T ناتهی است و بوضوح  نتیجه اینکه T زیرمجموعه ای ناتهی از مجموعه اعداد طبیعی است و لذا بنا بر اصل خوشترتیبی T دارای عضو مینیممی چون  است. 

حال چون 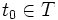 پس با توجه به تعریف مجموعه T داریم: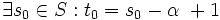 

 

اکنون ادعا می کنیم 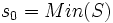 چرا که: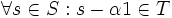 

 
و 
 

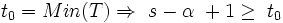
پس: 

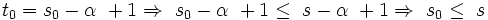
به این ترتیب 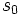 مینیمم S است چون کوچکتر یا مساوی هر عضو دلخواه از S است. 

به این ترتیب نشان دادیم S دارای عضو ابتدا یا مینیمم است و حکم ثابت می شود.

2- هر زیر مجموعه ناتهی از بالا کراندار از مجموعه اعداد صحیح دارای عضو ماکزیمم است. 

برهان: 

فرض می کنیم مجموعه S زیر مجموعه ای ناتهی و از بالا کرانداری از مجموعه اعدا صحیح باشد. نشان میدهیم S دارای عضو ماکزیمم است یعنی:  
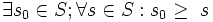
مجموعه T را به این صورت تعریف می کنیم: 
 
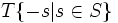
در این صورت چون مجموعه S ناتهی است T نیز ناتهی است و چون S از بالا کراندار است لذا T از پایین کراندار است. 
همچنین T زیرمجموعه ای از اعداد صحیح است. پس بنا بر مطلب قبل T زیرمجموعه ای ناتهی و از پایین کرانداری از مجموعه اعدا صحیح است و لذا دارای عضو مینیمم است. 
 
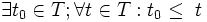
و چون 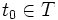 با توجه به تعریف مجموعه T میتوان نتیجه گرفت: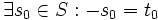 
 
حال ادعا می کنیم 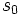 عضو ماکزیمم مجموعه S است چون: 
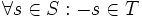 و چون  مینیمم عضو مجموعه T است پس: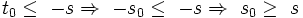 
 و این نشان می دهد برای هر عضو دلخواه s از مجموعه S عضو  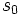بزرگتر یا مساوی s است پس  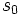ماکزیمم عضو مجموعه S است. 
به این ترتیب نشان دادیم مجموعه S دارای عضو ماکزیمم است و حکم ثابت می شود.