در ریاضیات بزرگترین مقسوم علیه مشترک یا ب.م.مِ دو عدد صحیح، به بزرگترین عدد طبیعی گفته میشود که آن دو عدد را میشمارد.
بزرگترین مقسوم علیه مشترک میان دو عدد طبیعی  و
و 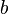 بصورت
بصورت 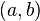 یا
یا  نوشته میشود.
نوشته میشود.
مثال:  و
و 
هرگاه ب.م.م دو عدد برابر ۱ باشد، آن دو عدد را نسبت بههم اول میگوئیم.
مثال: دو عدد ۱۴ و ۵ نسبت به هم اول هستند، زیرا، داریم 
ب.م.م برای ساده تر کردن کسرها نیز مفید است. برای مثال:

...
محاسبه ب.م.م:
روش تجزیه به عوامل اول:
اصولاً میتوان ب.م.م دو عدد را با تجزیه عددها به فاکتورهای اولشان پیدا کرد. برای مثال:
۲٫۳۲=۱۸ و ۳٫۷.۲۲=۸۴
مشاهده می کنید که فاکتورهای مشترک این دو عدد ۲ و ۳ هستند پس: gcd(۸۴٬۱۸) = ۲٫۳ = ۶
محاسبه ب.م.م به این روش فقط برای اعداد کوچک عملی است و برای اعداد بزرگتر زمان بسیاری نیاز دارد.
روش اقلیدسی:
یکی از بهترین روشها برای محاسبهٔ ب.م.م الگوریتم اقلیدس است که از الگوریتم تقسیم استفاده میکند.
مثال: یافتن (۸۴٬۱۸)gcd
ابتدا ۸۴ را به ۱۸ تقسیم می کنیم؛ خارج قسمت تقسیم ۴ و باقیمانده ۱۲ بدست میآید.
سپس ۱۸ را بر ۱۲ تقسیم می کنیم؛ خارج قسمت ۱ و باقیمانده ۶ بدست میآید؛ مجدداً ۱۲ را بر ۶ تقسیم میکنیم؛ خارج قسمت ۲ و باقیمانده ۰ میشود. پس عدد ۶ ب.م.م دو عدد ۸۴ و ۱۸ است.
در روش اقلیدسی اصطلاحاً خارج قسمت را بطور متوالی می شکنیم تا به باقیمانده ۰ برسیم.
خاصیتهای ب.م.م:
- هر مقسوم علیه دو عدد a و b، مقسوم علیه (gcd(a،b نیز هست.
- ب.م.م دو عدد a و ۰ برابر |a| است. |gcd(a،۰)=|a.
- اگر a مقسوم علیه b.c باشد و داشته باشیم gcd(a، b) = d آنگاه a/d مقسوم علیه c است.
- اگر m یک عدد نامنفی باشد آنگاه داریم: (gcd(m·a، m·b) = m·gcd(a، b.
- اگر m یک عدد صحیح باشد آنگاه داریم: (gcd(a + m·b، b) = gcd(a، b.
- اگر m مقسوم علیه مشترک غیر صفر a و b باشد آنگاه داریم: gcd(a/m، b/m) = gcd(a، b)/m
- ب.م.م دارای خاصیت جابجایی است؛ (gcd(a، b) = gcd(b، a
- ب.م.م دارای خاصیت شرکتپذیری است؛ (gcd(a، gcd(b، c)) = gcd(gcd(a، b)، c
- ب.م.م دو عدد a و b وقتی که هیچ کدام ۰ نباشند، تعریف میشود: کوچکترین عدد مثبت d بشکلی که بتوان به فرم d = a·p + b·q نوشت که در آن p و q اعداد صحیح هستند.

