تابع محدب

تابع محدب بر یک بازه:

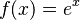اگر تابع پیوسته $f$ دارای این خاصیت باشد که در فاصلهٔ هر دو نقطه، نمودار تابع زیر وتر بین دو نقطه باشد، گوییم $f$ یک تابع محدب است یا تحدب $f$ به سمت پایین است. توابع $f(x)=x^2$ و تابع نمایی $f(x)=e^x$ دو مثال آشنا از توابع محدب هستند. بسیاری از نابرابری‌های متداول در آنالیز ریاضی ریشه در تحدب دارند. نابرابری‌های ینسن، هولدر، مینکوفسکی چند نمونه از این نابرابری‌ها هستند.

تعریف:

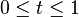فرض کنیم $-\infty\le a<b\le+\infty$ ، تابع $f:(a,b)\to \mathbb R$ را محدب گوییم در صورتی که به ازای هر دو عدد $x_1,x_2\in(a,b)$ و هر $t$ که $0\le t\le1$ ، داشته باشیم:

$f(tx_1+(1-t)x_2)\leq t f(x_1)+(1-t)f(x_2)$

اگر در تعریف بالا تساوی را برداریم آنگاه $f$ را اکیداً محدب می‌نامیم.

منبع: از ویکی‌پدیا، دانشنامهٔ آزاد

تعریف هندسی توابع چندمتغیره‌ی «محدب»:

فرض کنید تابع ‌f یک تابع چندمتغیره بر روی مجموعه‌ی «محدب» S باشد:

تابع مذکور زمانی «محدب» است که خط واصل بین دو نقطه از منحنی f به‌هیچ وجه از نقطه‌ یا نقاطی پایین منحنی عبور ننماید.

یاداوری – تنها توابع تعریف شده بر روی مجموعه‌های «محدب» در این تعاریف جای می‌گیرند.

مجموعه محدب:
گوییم $5c2f3b6a2c21319f848db759f05b345a$ مجموعهای محدب است، اگر هر ترکیب محدب از هر دو عضو $8ce4b16b22b58894aa86c421e8759df3$ همچنان عضو $8ce4b16b22b58894aa86c421e8759df3$ باشد. یعنی اگر $cb5cc348a373d06952132117ba10f0b3$ و $e77f292ab6acc4c2757bd58e3bfe2cef$ آنگاه به ازای هر $1e7fffc2c1cba34188529b70396467a1$ داشته باشیم $18c1f3a2bf572c9396d5d41007d4c402$ .

مجموعه محدب

مجموعه غیر محدب

تعریف هندسی توابع چندمتغیره ی «محدب»
فرض کنید تابع $Com Math 04920 12$ یک تابع چندمتغیره بر روی مجموعه ی «محدب» $Com Math 04920 1$ باشد:

- تابع مذکور زمانی «مقعر» است که خط واصل بین دو نقطه از منحنی $Com Math 04920 12$ به هیچ وجه از نقطه یا نقاطی بالای منحنی عبور نکند.
- تابع مذکور زمانی «محدب» است که خط واصل بین دو نقطه از منحنی $Com Math 04920 12$ به هیچ وجه از نقطه یا نقاطی پایین منحنی عبور ننماید.
این تعریف همانند تعریف توابع یک متغیره ی «محدب» است.یادآوری – تنها توابع تعریف شده بر روی مجموعه های «محدب» در این تعاریف جای میگیرند.

تعریف ریاضی توابع چندمتغیره ی «محدب»
فرض کنید $Com Math 04920 12$ تابعی چند متغیره بر روی مجموعه ی «محدب» $Com Math 04920 1$ باشد:

- تابع $Com Math 04920 12$ زمانی «مقعر» است که برای هر $Com Math 04920 13$ و هر $Com Math 04920 14$ و همه ی $Com Math 04920 15$ داشته باشیم:

$Com Math 04920 16$

(رابطه ی 2)
- تابع $Com Math 04920 12$ زمانی «محدب» است که برای هر $Com Math 04920 13$ و هر $Com Math 04920 14$ و همه ی $Com Math 04920 15$ داشته باشیم:

$Com Math 04920 17$

http://anymath.ir

انجمن دبیران ریاضیات

انجمن دبیران ریاضیات