در ریاضیات، ریشه دوم یا جذر یک عدد حقیقی غیرمنفی  به صورت
به صورت 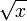 نشان داده میشود و نتیجه آن عددی حقیقی غیر منفی است که مجذورش (عدد حاصل از ضرب یک عدد در خودش)[۱] برابر
نشان داده میشود و نتیجه آن عددی حقیقی غیر منفی است که مجذورش (عدد حاصل از ضرب یک عدد در خودش)[۱] برابر  است.
است.
برای مثال، جذر عدد ۹ برابر ۳ است (به صورت 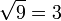 نمایش مییابد) زیرا داریم
نمایش مییابد) زیرا داریم 
جذر اغلب در هنگام حل معادله درجه دوم و یا معادلههای به شکل  استفاده میشود، زیرا متغیر
استفاده میشود، زیرا متغیر  به توان دو رسیدهاست.
به توان دو رسیدهاست.
طبق قانون بنیادی جبری، دو جواب برای ریشه دوم یک عدد وجود دارد (این دو جواب در ریشه دوم عدد صفر با هم یکی هستند). برای هر عدد حقیقی مثبت دو جواب برای ریشه دوم وجود دارد که این دو جواب عددی هستند که یک بار منفی و یک بار مثبت است (به شکل  ).
).
ریشه دوم اعدادی که مربع کامل نیستند همواره عددی گنگ است، یعنی اعداد را نمیتوان به صورت کسری از دو عدد صحیح گویا کرد. برای مثال،  را نمیتوان دقیقاً به صورت m/n نوشت، که در آن n و m اعدادی صحیح هستند. در هر حال این عدد اندازه قطر مربعی به ضلع یک است. از مدتهای گذشته، عدد
را نمیتوان دقیقاً به صورت m/n نوشت، که در آن n و m اعدادی صحیح هستند. در هر حال این عدد اندازه قطر مربعی به ضلع یک است. از مدتهای گذشته، عدد  را عددی گنگ میدانستند و آن را به فیثاغورث نسبت میدادند.
را عددی گنگ میدانستند و آن را به فیثاغورث نسبت میدادند.
نماد ریشه دوم ( ) برای اولین بار در قرن شانزدهم استفاده شد. به نظر میرسد که این علامت از حرف کوچک r برگرفته شدهاست، که بیانگر واژه لاتین radix به معنای ریشه است.
) برای اولین بار در قرن شانزدهم استفاده شد. به نظر میرسد که این علامت از حرف کوچک r برگرفته شدهاست، که بیانگر واژه لاتین radix به معنای ریشه است.
خواص
- تابع ریشه دوم،
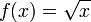 ، تابعی است از مجموعه اعداد حقیقی غیرمنفی
، تابعی است از مجموعه اعداد حقیقی غیرمنفی  به خودش.
به خودش.
- تابع ریشه دوم
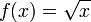 همواره مقداری منحصربهفرد برمی گرداند.
همواره مقداری منحصربهفرد برمی گرداند.
- برای به دست آوردن هر دو جواب ریشه دوم، ابتدا اولین جواب را به دست آورید و آن را x1 بنامید، سپس آن را از صفر کم کنید تا x2 به دست آید (x2 = 0 − x1).
- خواص زیر، مهمترین خواص ریشه دوم هستند که برای هر عدد حقیقی مثبت
 و
و  صحیح هستند:
صحیح هستند:
- ریشه دوم تابعی است از اعداد گویا به اعداد جبری.
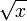 عددی گویا است، اگر و تنها اگر
عددی گویا است، اگر و تنها اگر  عددی گویا باشد که بتوان آن را به صورت کسری از دو عدد مربع کامل نشان داد. به طور کلی،
عددی گویا باشد که بتوان آن را به صورت کسری از دو عدد مربع کامل نشان داد. به طور کلی،  عددی گنگ است.
عددی گنگ است.
- در هندسه، تابع ریشه دوم نگاشتی از سطح یک مربع به طول اضلاعش.
- بر خلاف عقیده همه،
 لزوماً برابر
لزوماً برابر  نیست. این برابری تنها در مواردی که
نیست. این برابری تنها در مواردی که  غیرمنفی باشد صدق میکند. اما اگر
غیرمنفی باشد صدق میکند. اما اگر 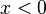 باشد، طبق تعریف
باشد، طبق تعریف  است و این یعنی
است و این یعنی  . در نتیجه برای هر عدد حقیقی
. در نتیجه برای هر عدد حقیقی  داریم
داریم  . (قدرمطلق را ببینید)
. (قدرمطلق را ببینید)
- فرض کنید
 و
و  اعدادی حقیقی هستند به طوری که
اعدادی حقیقی هستند به طوری که  ، و ما میخواهیم که
، و ما میخواهیم که  را بیابیم. یکی از اشتباهات رایج این است که آن را به «معادله جذر» تبدیل کنیم و از آن
را بیابیم. یکی از اشتباهات رایج این است که آن را به «معادله جذر» تبدیل کنیم و از آن  را نتیجه بگیریم. این کار نادرست است، زیرا ریشه دوم
را نتیجه بگیریم. این کار نادرست است، زیرا ریشه دوم  برابر
برابر  نیست، بلکه
نیست، بلکه  است (طبق یکی از خاصیتهای فوق). اما ما میتوانیم بگوییم
است (طبق یکی از خاصیتهای فوق). اما ما میتوانیم بگوییم  ، و در نتیجه
، و در نتیجه  .
.
- در حسابان، مثلاً وقتی میخواهیم اثبات کنیم که تابع ما پیوسته یا مشتقپذیر و یا قابل حدگیری است، میتوانیم از عبارت زیر استفاده کنیم:
این عبارت برای تمام  و
و  های نامنفی به طوری که هر دو صفر نباشند صحیح است.
های نامنفی به طوری که هر دو صفر نباشند صحیح است.
- نمودار تابع
 به شکل زیر است، این نمودار از نصف یک سهمی ساخته میشود:
به شکل زیر است، این نمودار از نصف یک سهمی ساخته میشود:

- تابع در تمام
 های غیرمنفی پیوسته و برای تمام
های غیرمنفی پیوسته و برای تمام  های مثبت مشتقپذیر است. (در
های مثبت مشتقپذیر است. (در  مشتقپذیر نیست، زیرا شیب نمودار یا همان تانژانت در این نقطه ∞ است) مشتق این تابع برابر است با:
مشتقپذیر نیست، زیرا شیب نمودار یا همان تانژانت در این نقطه ∞ است) مشتق این تابع برابر است با:
- در سری تیلور
 در
در  و برای
و برای  میتوان از بسط نیوتن استفاده کرد:
میتوان از بسط نیوتن استفاده کرد:
 |  |
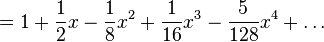 |
امروزه روشهای بسیاری برای محاسبه ریشه دوم وجود دارد، بعضی از آنها را میتوان بر روی کاغذ انجام داد و بعضی از آنها هم با ماشین، البته همه ماشینحسابها دارای دکمه رادیکال نیستند.
اغلب برای حساب کردن ریشه دوم از بعضی برنامههای صفحهگسترده کامپیوتر و برخی دیگر از نرمافزارها استفاده میشود. نرمافزارهای کامپیوتری قابلیت محاسبه توابع نمایی و لگاریتم طبیعی را دارند و با استفاده از آن ریشه دوم  را محاسبه مینمایند، به شکل زیر:
را محاسبه مینمایند، به شکل زیر:

برای محاسبه ریشه دوم میتوان از خطکش مهندسی یا جدول لگاریتم کمک گرفت.
رایجترین روش محاسبه ریشه دوم بر روی کاغذ، استفاده از «روش بابلی» است. این روش از یک عملیات ساده استفاده میکند، و هر چه این روش را بیشتر انجام دهید به جواب نزدیکتر خواهید شد. برای پیدا کردن  ، ریشه دوم عدد
، ریشه دوم عدد  :
:
- عددی تصادفی انتخاب کنید که اگر به توان دو برسد به عدد
 نزدیکتر باشد. (بهترین عدد، نزدیکترین عدد کمتر از
نزدیکتر باشد. (بهترین عدد، نزدیکترین عدد کمتر از  است)
است) - جای
 را با میانگین
را با میانگین  و x / r عوض کنید.
و x / r عوض کنید. - مراحل ۲ و ۳ را تکرار کنید.
در وضعیتهایی که بخواهیم تعداد بی شمار ریشه دوم یک عدد را به دست آوریم، مانند:
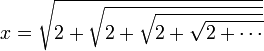
جواب یک عدد گویاست. عدد گویا را میتوان با قرار دادن
 در زیر رادیکال به دست آورد به صورت:
در زیر رادیکال به دست آورد به صورت:
اگر این سئوال را حل میکنیم، به جواب x = ۲ میرسیم. از این تقریب میتوانیم در هر جایی که n > ۰ استفاده کنیم:

همین رویه را میتوان به صورت زیر داشت:

این روش برای تمام مقادیر
 ، یک مقدار
، یک مقدار  گویا میدهد، مانند:
گویا میدهد، مانند:
ریشه دوم بیست عدد صحیح مثبت


۱ 

۱٫۴۱۴۲۱۳۵۶۲۳ ۷۳۰۹۵۰۴۸۸۰ ۱۶۸۸۷۲۴۲۰۹ ۶۹۸۰۷۸۵۶۹۶ ۷۱۸۷۵۳۷۶۹۴ ۸۰۷۳۱۷۶۶۷۹ ۷۳۷۹۹۰۷۳۲۴ ۷۸۴۶۲ 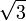

۱٫۷۳۲۰۵۰۸۰۷۵ ۶۸۸۷۷۲۹۳۵۲ ۷۴۴۶۳۴۱۵۰۵ ۸۷۲۳۶۶۹۴۲۸ ۰۵۲۵۳۸۱۰۳۸ ۰۶۲۸۰۵۵۸۰۶ ۹۷۹۴۵۱۹۳۳۰ ۱۶۹۰۹ 

۲ 

۲٫۲۳۶۰۶۷۹۷۷۴ ۹۹۷۸۹۶۹۶۴۰ ۹۱۷۳۶۶۸۷۳۱ ۲۷۶۲۳۵۴۴۰۶ ۱۸۳۵۹۶۱۱۵۲ ۵۷۲۴۲۷۰۸۹۷ ۲۴۵۴۱۰۵۲۰۹ ۲۵۶۳۸ 

۲٫۴۴۹۴۸۹۷۴۲۷ ۸۳۱۷۸۰۹۸۱۹ ۷۲۸۴۰۷۴۷۰۵ ۸۹۱۳۹۱۹۶۵۹ ۴۷۴۸۰۶۵۶۶۷ ۰۱۲۸۴۳۲۶۹۲ ۵۶۷۲۵۰۹۶۰۳ ۷۷۴۵۷ 

۲٫۶۴۵۷۵۱۳۱۱۰ ۶۴۵۹۰۵۹۰۵۰ ۱۶۱۵۷۵۳۶۳۹ ۲۶۰۴۲۵۷۱۰۲ ۵۹۱۸۳۰۸۲۴۵ ۰۱۸۰۳۶۸۳۳۴ ۴۵۹۲۰۱۰۶۸۸ ۲۳۲۳۰ 

۲٫۸۲۸۴۲۷۱۲۴۷ ۴۶۱۹۰۰۹۷۶۰ ۳۳۷۷۴۴۸۴۱۹ ۳۹۶۱۵۷۱۳۹۳ ۴۳۷۵۰۷۵۳۸۹ ۶۱۴۶۳۵۳۳۵۹ ۴۷۵۹۸۱۴۶۴۹ ۵۶۹۲۴ 

۳ 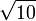

۳٫۱۶۲۲۷۷۶۶۰۱ ۶۸۳۷۹۳۳۱۹۹ ۸۸۹۳۵۴۴۴۳۲ ۷۱۸۵۳۳۷۱۹۵ ۵۵۱۳۹۳۲۵۲۱ ۶۸۲۶۸۵۷۵۰۴ ۸۵۲۷۹۲۵۹۴۴ ۳۸۶۳۹ 

۳٫۳۱۶۶۲۴۷۹۰۳ ۵۵۳۹۹۸۴۹۱۱ ۴۹۳۲۷۳۶۶۷۰ ۶۸۶۶۸۳۹۲۷۰ ۸۸۵۴۵۵۸۹۳۵ ۳۵۹۷۰۵۸۶۸۲ ۱۴۶۱۱۶۴۸۴۶ ۴۲۶۰۹ 

۳٫۴۶۴۱۰۱۶۱۵۱ ۳۷۷۵۴۵۸۷۰۵ ۴۸۹۲۶۸۳۰۱۱ ۷۴۴۷۳۳۸۸۵۶ ۱۰۵۰۷۶۲۰۷۶ ۱۲۵۶۱۱۱۶۱۳ ۹۵۸۹۰۳۸۶۶۰ ۳۳۸۱۸ 

۳٫۶۰۵۵۵۱۲۷۵۴ ۶۳۹۸۹۲۹۳۱۱ ۹۲۲۱۲۶۷۴۷۰ ۴۹۵۹۴۶۲۵۱۲ ۹۶۵۷۳۸۴۵۲۴ ۶۲۱۲۷۱۰۴۵۳ ۰۵۶۲۲۷۱۶۶۹ ۴۸۲۹۳ 

۳٫۷۴۱۶۵۷۳۸۶۷ ۷۳۹۴۱۳۸۵۵۸ ۳۷۴۸۷۳۲۳۱۶ ۵۴۹۳۰۱۷۵۶۰ ۱۹۸۰۷۷۷۸۷۲ ۶۹۴۶۳۰۳۷۴۵ ۴۶۷۳۲۰۰۳۵۱ ۵۶۳۰۷ 

۳٫۸۷۲۹۸۳۳۴۶۲ ۰۷۴۱۶۸۸۵۱۷ ۹۲۶۵۳۹۹۷۸۲ ۳۹۹۶۱۰۸۳۲۹ ۲۱۷۰۵۲۹۱۵۹ ۰۸۲۶۵۸۷۵۷۳ ۷۶۶۱۱۳۴۸۳۰ ۹۱۹۳۷ 

۴ 

۴٫۱۲۳۱۰۵۶۲۵۶ ۱۷۶۶۰۵۴۹۸۲ ۱۴۰۹۸۵۵۹۷۴ ۰۷۷۰۲۵۱۴۷۱ ۹۹۲۲۵۳۷۳۶۲ ۰۴۳۴۳۹۸۶۳۳ ۵۷۳۰۹۴۹۵۴۳ ۴۶۳۳۸ 

۴٫۲۴۲۶۴۰۶۸۷۱ ۱۹۲۸۵۱۴۶۴۰ ۵۰۶۶۱۷۲۶۲۹ ۰۹۴۲۳۵۷۰۹۰ ۱۵۶۲۶۱۳۰۸۴ ۴۲۱۹۵۳۰۰۳۹ ۲۱۳۹۷۲۱۹۷۴ ۳۵۳۸۶ 

۴٫۳۵۸۸۹۸۹۴۳۵ ۴۰۶۷۳۵۵۲۲۳ ۶۹۸۱۹۸۳۸۵۹ ۶۱۵۶۵۹۱۳۷۰ ۰۳۹۲۵۲۳۲۴۴ ۴۹۳۶۸۹۰۳۴۴ ۱۳۸۱۵۹۵۵۷۳ ۲۸۲۰۳ 

۴٫۴۷۲۱۳۵۹۵۴۹ ۹۹۵۷۹۳۹۲۸۱ ۸۳۴۷۳۳۷۴۶۲ ۵۵۲۴۷۰۸۸۱۲ ۳۶۷۱۹۲۲۳۰۵ ۱۴۴۸۵۴۱۷۹۴ ۴۹۰۸۲۱۰۴۱۸ ۵۱۲۷۶ در هند باستان، استفاده از ریشه دوم به سولبا سوتراس برمی گردد، که حدود ۵۰۰-۸۰۰ سال قبل از میلاد بودهاست. اولین روش برای یافتن ریشه دوم عدد ۲ و ۳ توسط بودایانا سولبا سوترا ارائه شده بود. آریاباتا در آریاباتیا (قسمت ۲٫۴) هم روشی برای به دست آوردن ریشه دوم اعداد چندرقمی داده بود.
د. ا. اسمیت در کتاب تاریخ ریاضی گفتهاست، «در اروپا چنین روشهایی (برای پیدا کردن ریشه دوم و مربع یک عدد) قبل از کاتنو (۱۵۴۶) استفاده نمیشدهاست. او روشهایی را برای به دست آوردن ریشه دوم، با استفاده از روش آریاباتا ارائه کرده بود.»
- منبع : دانشنامه ویکی پدیا






