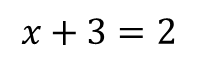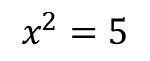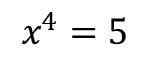یافتن ریشه ی معادلات

تعریف معادله رو کم و بیش هممون می دونیم.

یعنی تساوی دو مقدار که ممکنه در طرفین تساوی، یک یا چند مقدار مجهول داشته باشیم.

خوارزمی دانشمند و ریاضیدان ایرانی، در کتاب الجبر و المقابله ی خودش، معادلاتی مثلا از درجه ی یک رو به شکل زیر حل می کرد:

به طور مثال اگه معادله ای به شکل زیر داشته باشیم، می تونیم مقدار x رو به راحتی بدست بیاریم:

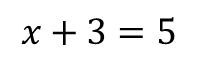
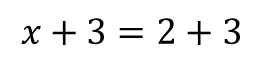
و 3 رو از طرفین تساوی حذف می کرد و مقدار

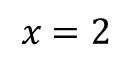
رو بدست می اورد و به همین ترتیب معادلات دیگه رو

می دونید ایده ی این کار رو از کجا می آورد؟

قبل از اینکه وارد مقوله ی تعیین ریشه ی معادلات بریم، اجازه بدید یه کوچولو درباره ی دیدگاه گذشتگان درباره ی اعداد صحبت کنیم:

در گذشته، بالاخص در یونان، ریاضی رو اکثرا هندسه می دونستن.

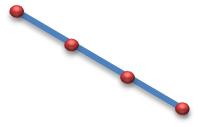
به همین خاطر اعداد رو به شکل طول یه خط می دیدند.

مثلا عدد سه رو به شکل زیر می دیدن:

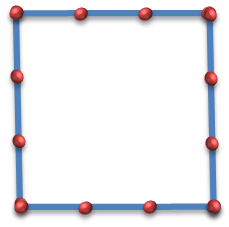
پس 3 به توان 2 می شه مساحت مربعی به طول 3:

و به همین ترتیب، 3 به توان 3، میشه حجم مکعبی به طول 3:

دقت کردید که چرا ریاضیدانان گذشته، مثل ارشمیدس و ... و یا حتی ریاضیدانای ایرانی با این همه نبوغ، سعی نکردند که معادلات بالاتر از درجه ی سوم رو بررسی کنن؟

برای اینکه اونا بالاتر از درجه ی سوم رو نمی تونستن تصور کنند.چون اعداد رو فقط به صورت هندسی تصور می کردند و به همین علت چون تصور درجه ی چهارم (بعد چهارم) غیر ممکن بود، بنابراین به به اعدادی به توان 4 به هیچ عنوان فکر نمی کردند.

با این اوصاف، چندین اشکال به این نوع دیدگاه وارد میشه:

1.عدم وجود اعداد با توان های بالاتر از 3

2.عدم وجود اعداد منفی

3.عدم وجود اعداد غیر طبیعی (مثل اعداد گنگ مثل رادیکال 2 و ...)

و ...

پس با این حال معادلاتی مثل زیر غیر قابل فهم بودند: