معادله چند جمله یی :

که در آن

، در 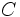جواب
دارد. به عبارت دیگر
•
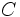
از لحاظ جبری بسته است
معادله بالا را معادله چند جمله یی از درجه
( هنگامی که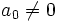
) گویند. از قضیه بنیادی جبر نتیجه می‌شود که:

فرع 1.

معادله چند جمله یی، درجه ،
با احتساب ریشه های مکرر،‌
ریشه در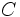
دارد.

اثبات در ادامه نوشته...!

مثال؛

معادله درجه سوم
را حل کنید.
حل.
می‌نویسیم ،
پس، چون

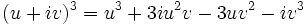
باید داشته باشیم

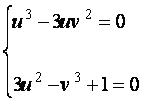
از معادله اول نتیجه می‌شود

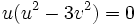
پس

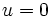
یا

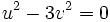
وقتی ،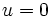
از معادله دوم نتیجه می‌شود:

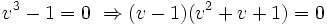
چون ،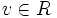
،
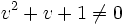لذا .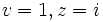
هنگامی که
، .
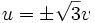از قرار دادن این مقدار در معادله دوم خواهیم داشت

چون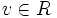
،
و لذا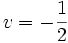
پس

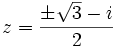
و

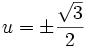
بنابراین سه ریشه به دست می‌آید

ک.ف گاوس (1777-1855 ) دررساله اش چندین
استدلال برای قضیه بنیادی جبر داده است. خوانندگان علاقه مند به این استدلالها
می‌توانند به کتابهای درسی استانده در آنالیز مختلط مانند: آنالیز مختلط اثر باک و
نیومن و جاذبه‌های آنالیز مختلط اثر بوآز مراجعه نمایند.
باید توجه داشت که
قضیه بنیادی جبر به وجود جوابها در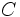حکم
می‌کند ولی از چگونگی پیدا کردن آنها صحبتی به میان نمی‌آورد. در واقع هیچ گونه
دستور جبری کارساز برای یک چند جمله یی غیر مشخصی از درجه 5 ( یا بالاتر ) وجود
ندارد .

...خدایا....
من به تو اعتماد میکنم که رمز ایمان واقعی من است...